Modeling credit card interest

Lesson 2W

The credit card interest problem

Here is the problem from class: You owe $2000 on a credit card with 13% annual interest. You pay $50 per month. Assuming interest and payments happen continuously, how long does it take to pay off the credit card?

We discussed in class that if \(t\) is measured in years, and \(M\) represents the account balance, then the differential equation is \[M’=0.13M - 600.\]

The \(0.13M\) in the equation is the interest you pay. We say that the interest is proportional to the account balance. So if you have twice as much money in your account, you get twice as much interest. Any time that a quantity changes proprtionally to its value, we call it exponential growth (or decay). If not for the $50 per month we are paying on this credit card, our account balance would grow exponentially.

What if interest is compounded monthly?

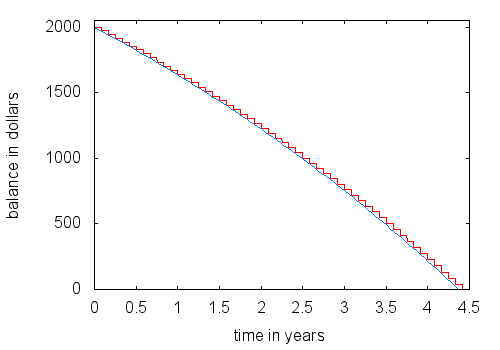
You may be curious about what would happen if we didn’t make the assumption that interest was compounded continuously and payments were made continuously. If you make payments once a month and interest is compounded monthly, it is much more complicated to compute the account balance. There is no good formula—you just have to make a table and compute each month’s balance from the one before it. If you do this, you will find that you pay off the balance in 4 years and 5 months, with the last month’s payment being $35.

If you assume interest is compounded continuously, you pay off the balance after 4 years and 4.4 months. After a year, the two fomulas for account balance differ by $2.08. After 4 years and 4 months, the difference in balance is $14.27.

Here is a graph comparing the account balances calculated using the two different methods.

Limit as t goes to infinity

Someone pointed out to me that as \(t\to\infty\), the account balance goes to \(-\infty\). This is a good observation, and clearly not what would happen in real life. What causes our model to stop working?

Class Wednesday

In class on Wednesday, you will work together on the homework from section 2.3. I recommend finishing the two ungraded problems before class, so that you can spend class working on the graded problems.